闵行中学高中一年级期末数学试题
2018.06
1、 填空题
1. 计算
__________
2. 察看下列等式：
，
，
，
，可以猜想
__________
3. 若
，则
______________________________
4. 函数
最小正周期为
，其中
，则
______________________________
5. 在等差数列
中，已知，，则__________
6. 在等比数列中，已知，，则__________
7. 函数
的最小值是__________
8. 无穷等比数列，若
，各项之和为
，则公比__________
9. !
的三边分别为a、b、c，已知
，
，
，则边长
__________
10. 已知
，则__________
11. 在!，给出下列四个命题：
① 若，
，
，则该三角形有且仅有两解；
② 若三角形的三边长的比是，则此三角形的最大角为
；
③ 若
为锐角三角形，且三边长分别为2、3、，则的取值范围是
；④ 若
，则角A的取值范围是
.
其中所有正确命题的序号是__________
12. 将正偶数集合
从小到大按第n组有2n个偶数进行分组，第一组：
，第
二组：，第三组：，…，则2018坐落于第__________组
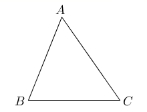13. 为了竖一块广告牌，要制造三角形支架，如图，需要
，BC的长度大于1米，且AC比AB长0.5
米，为了稳定广告牌需要AC越短越好，则AC最短为
__________米
14. 已知
为数列的前n项和，且
，
，则的首项的所大概值为__________
2、 选择题
15. “
”是“”的（ ）
A. 充分非必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也非必要条件
16. 在数列中，假如
，那样使这个数列的前n项和获得最大值时n的值为（ ）
A. 19 B. 20 C. 21 D. 22
17. 在等差数列中，已知
，
，则（ ）
A. 
B. 
C. 
D.
18. 将的图像向右平移
个单位后得到的图像的一条对称轴是（ ）
A. B. C. D. 
19. 若是等差数列，则下列数列中仍为等差数列的个数有（ ）
① 
；② 
；③ ；④ 
.
A. 1个 B. 2个 C. 3个 D. 4个
20. 数列满足
，
，若数列的前n项
和为，则的值为（ ）
A. 
B. C. 674 D. 2018
3、 解答卷
21. 在等差数列中，，.
（1）求数列的通项公式；（2）设的前n项和为，若
，求k.
22. 已知函数，.
（1）若
，求函数的值；（2）求函数的值域.
23. 设数列的前n项和为，在数列中，
，
.
（1）求和的通项公式；
（2）设
，求数列
前n项和
.
24. 某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的
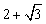
环境标志，小李、小王设计的底座形状分别为!ABC、!ABD，经测量米，
米，
米，.
（1）求AB的长度；
（2）若环境标志的底座每平米造价为5000元，
不考虑其他原因，小李、小王哪个的设计使建造费
用较低（请说明理由）？较低造价为多少？
25. 已知n为正整数，满足，
，设数列满足.
（1）求证：数列为等比数列；
（2）若数列是等差数列，求实数t的值；
（3）若数列是等差数列，前n项和为，对任意的，均存在，使得
成立，求满足条件的所有整数的值.
参考答案
1、 填空题
1. 3 2. ， 3. 4. 6 5. 6.
7. 5 8. 
9. 
10. 
11. ②③④ 12. 32
13. 14.
2、 选择题
15. A 16. B 17. D 18. C 19. C 20. C
3、 解答卷
21.（1）；（2）
.
22.（1），，；（2）.
23.（1），，；（2）错位相减，.
24.（1）
，∴
；（2）小李，
，.
25.（1）公比为2；（2）；（3），
.
